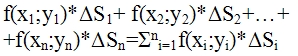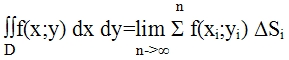1. Двойной интеграл.

("дельта" - это тупо треугольничек)
Пусть в замкнутой области D в плоскости Oxy задана функция 2-х переменных Z=f(x;y). Разобьем область D на n элементарных частей. Di, где i = 1, 2, …, n. (дельта)Si - площади частей, di (d итое) - диаметры частей.

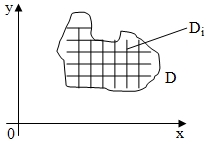
В каждой области Di выберем произвольную точку Mi (xi;yi). Умножим значение f(xi;yi) на (дельта)Si. Составим сумму таких произведений.

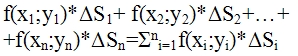
Эта сумма называется интегральной суммой функции z=f(x;y) в области D. Рассмотрим предел этой суммы, когда n стремится к бесконечности. В этом случае di->0. Если этот предел существует и не зависит от способа разветвления области D на части, не зависит от выбора точек в этих частях, то он называется двойным интегралом от функции f(x;y) по области D и обозначается

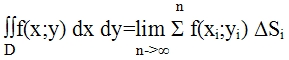
Функция f(x;y) называется интегрируемой функцией области D. Область D называется областью интегрирования. x и y - переменными интегрирования. dx*dy=ds - элемент площади интегрирования.
Теорема. Достаточное условие интегрируемости функции: если функция z=f(x;y) непрерывна и замкнута в области D, то она интегрируема в этой области.