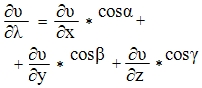13. Скалярное поле.
Скалярное поле - скалярная функция U=U(M) вместе с областью ее определения.
Характеризуется поверхностью уровня и линиями уровня. Поверхностью уровня скалярного поля называется геометрическое расположение точек, в которых функция 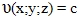 (1).
(1).
Через каждую точку поля проходит только одна поверхность уровня. Если в уравнение (1) подставим разное значение const, то получим различные поверхности уровня, которые как бы расслаивают поля.
Уравнение поверхности уровня можно найти путем подстановки координат точки в уравнение (1).
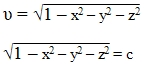
Поверхностью уровня данного уравнения является множество сфер.
При с=1 получим 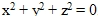 , то есть сфера стягивается в точку.
, то есть сфера стягивается в точку.
В случае плоского поля равенство (1) будет выглядеть 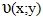 = с. Данное поле представляет собой линии поля, то есть линии уровня поля на плоскости, в точках которых функция
= с. Данное поле представляет собой линии поля, то есть линии уровня поля на плоскости, в точках которых функция 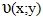 сохраняет линии уровня.
сохраняет линии уровня.
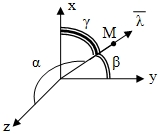
Для характеристики скорости изменения поля в заданном направлении введем понятие производной по направлению. Производной по направлению 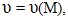 в точке M по направлению
в точке M по направлению 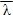 называется предел:
называется предел:
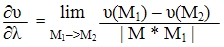

Производная по направлению 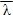 характеризует скорость изменения функции по этому направлению. Если
характеризует скорость изменения функции по этому направлению. Если 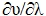 > 0, то функция
> 0, то функция 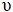 возрастает в направлении
возрастает в направлении 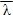 ; если
; если 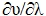 < 0, то функция убывает.
< 0, то функция убывает.
Модуль  представляет мгновенную скорость в точке M по направлению
представляет мгновенную скорость в точке M по направлению 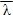 . Чем больше этот модуль, тем быстрее изменяется функция
. Чем больше этот модуль, тем быстрее изменяется функция 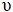 - в этом физический смысл производной по направлению.
- в этом физический смысл производной по направлению.
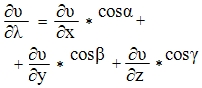
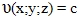 (1).
(1).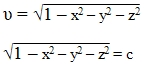
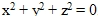 , то есть сфера стягивается в точку.
, то есть сфера стягивается в точку.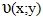 = с. Данное поле представляет собой линии поля, то есть линии уровня поля на плоскости, в точках которых функция
= с. Данное поле представляет собой линии поля, то есть линии уровня поля на плоскости, в точках которых функция 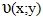 сохраняет линии уровня.
сохраняет линии уровня.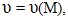 в точке M по направлению
в точке M по направлению 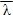 называется предел:
называется предел: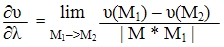

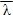 характеризует скорость изменения функции по этому направлению. Если
характеризует скорость изменения функции по этому направлению. Если 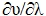 > 0, то функция
> 0, то функция 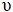 возрастает в направлении
возрастает в направлении 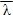 ; если
; если 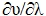 < 0, то функция убывает.
< 0, то функция убывает. представляет мгновенную скорость в точке M по направлению
представляет мгновенную скорость в точке M по направлению 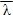 . Чем больше этот модуль, тем быстрее изменяется функция
. Чем больше этот модуль, тем быстрее изменяется функция 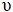 - в этом физический смысл производной по направлению.
- в этом физический смысл производной по направлению.