14. Градиент скалярного поля
Вектор, называемый градиентом скалярного поля, указывает направление вектора 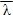 , в котором произведение
, в котором произведение 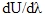 имеет наибольшее значение.
имеет наибольшее значение.
Вектор, координатами которого являются значения частных производных функции U(x;y) в т. M(x;y;z) - градиент функции grad U.
Свойства:
1. grad направлен по нормали к поверхности уровня, проходящей через точку 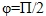 .
.
2. grad (U+V) = grad U + grad V
3. grad (c*U) = c*grad U (c-const)
4. grad (U*V) = U*grad V + V*grad U
5. grad (U / V) = (V*grad U - U*grad V) / V*2
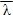 , в котором произведение
, в котором произведение 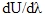 имеет наибольшее значение.
имеет наибольшее значение.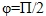 .
.