17. Числовые ряды. Необходимый признак сходимости ряда.
Числовые ряды - выражение типа
 (1)
(1)
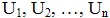 - члены ряда,
- члены ряда, 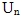 - общий член ряда.
- общий член ряда.
Ряд считается заданным, если задан общий член. Сумма первых n членов ряда называется n-ной суммой членов ряда.
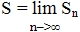
- называют суммой ряда (1) и говорят, что ряд сходится.
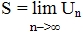
Если предел не существует, то ряд (1) считается расходящимся.
Свойства рядов:
1) Если ряд (1) сходится, то сходится и ряд 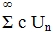 . (с - const)
. (с - const)
2) Если ряд (1) сходится и ряд 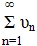 сходится, то
сходится, то 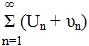 сходится.
сходится.
3) Если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходящиеся и расходящиеся одновременно.
Теорема (необходимый признак сходимости числового ряда). Если ряд (1) сходится, то его общий член стремится к нулю, то есть
 .
.
Если не выполняется, то расходится.
Достаточное условие расходимости ряда: если предел 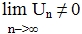 или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.
Необходимый признак сходимости ряда недостаточен для сходимости, поскольку существуют ряды, которые расходятся, но необходимый признак сходимости для них выполняется.
 (1)
(1)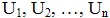 - члены ряда,
- члены ряда, 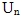 - общий член ряда.
- общий член ряда.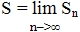
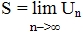
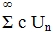 . (с - const)
. (с - const)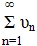 сходится, то
сходится, то 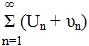 сходится.
сходится. .
.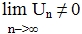 или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.