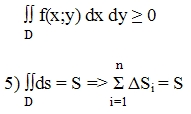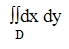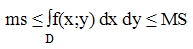2. Свойства двойного интеграла.



4) Если в области D имеет место неравенство f(x;y)>=0, то

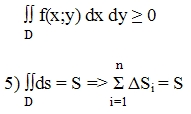
и наоборот. Иначе говоря, S плоской фигуры можно найти по формуле:

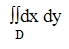
6) Если функция f(x;y) непрерывна в замкнутой области D, площадь которой равна S, то выполняется формула:

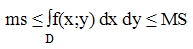
mS - минимальное значение, MS - максимальное значение подынтегральной функции в области D.

7) Если функция f(x;y) непрерывна в замкнутой области D, площадь которой равна S, то в этой области существует точка, координаты которой (x0,y0), что двойной интеграл области D равен площади:

- среднее значение функции f(x;y) в области D